2  Multiple Linear Regression

Read section 3.2 of the book before using these notes.

Note that in this course, lecture notes are not sufficient, you must read the book for better understanding. Lecture notes are just implementing the concepts of the book on a dataset, but not explaining the concepts elaborately.

2.1 Multiple Linear Regression

# importing libraries 
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

Develop a multiple linear regression model that predicts car price based on engine size, year, mileage, and mpg. Datasets to be used: Car_features_train.csv, Car_prices_train.csv

# Reading datasets
trainf = pd.read_csv('./Datasets/Car_features_train.csv')
trainp = pd.read_csv('./Datasets/Car_prices_train.csv')
train = pd.merge(trainf,trainp)
train.head()
carID brand model year transmission mileage fuelType tax mpg engineSize price
0 18473 bmw 6 Series 2020 Semi-Auto 11 Diesel 145 53.3282 3.0 37980
1 15064 bmw 6 Series 2019 Semi-Auto 10813 Diesel 145 53.0430 3.0 33980
2 18268 bmw 6 Series 2020 Semi-Auto 6 Diesel 145 53.4379 3.0 36850
3 18480 bmw 6 Series 2017 Semi-Auto 18895 Diesel 145 51.5140 3.0 25998
4 18492 bmw 6 Series 2015 Automatic 62953 Diesel 160 51.4903 3.0 18990

2.1.1 Training the model

#Using the ols function to create an ols object. 'ols' stands for 'Ordinary least squares'
ols_object = smf.ols(formula = 'price~year+mileage+mpg+engineSize', data = train)
model = ols_object.fit()
model.summary()
OLS Regression Results
Dep. Variable: price R-squared: 0.660
Model: OLS Adj. R-squared: 0.660
Method: Least Squares F-statistic: 2410.
Date: Mon, 29 Jan 2024 Prob (F-statistic): 0.00
Time: 03:10:20 Log-Likelihood: -52497.
No. Observations: 4960 AIC: 1.050e+05
Df Residuals: 4955 BIC: 1.050e+05
Df Model: 4
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept -3.661e+06 1.49e+05 -24.593 0.000 -3.95e+06 -3.37e+06
year 1817.7366 73.751 24.647 0.000 1673.151 1962.322
mileage -0.1474 0.009 -16.817 0.000 -0.165 -0.130
mpg -79.3126 9.338 -8.493 0.000 -97.620 -61.006
engineSize 1.218e+04 189.969 64.107 0.000 1.18e+04 1.26e+04
Omnibus: 2450.973 Durbin-Watson: 0.541
Prob(Omnibus): 0.000 Jarque-Bera (JB): 31060.548
Skew: 2.045 Prob(JB): 0.00
Kurtosis: 14.557 Cond. No. 3.83e+07


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 3.83e+07. This might indicate that there are
strong multicollinearity or other numerical problems.

The model equation is: estimated car price = -3.661e6 + 1818 * year -0.15 * mileage - 79.31 * mpg + 12180 * engineSize

The procedure to fit the model using sklearn will be similar to that in simple linear regression.

model = LinearRegression()

X_train = train[['year','engineSize','mpg','mileage']] # Slice out the predictors
y_train = train[['price']]

model.fit(X_train,y_train)

2.1.2 Hypothesis test for a relationship between the response and a subset of predictors

Let us test the hypothesis if there is relationship between car price and the set of predictors: mpg and year.

hypothesis = '(mpg = 0, year = 0)'     
    
model.f_test(hypothesis) # the F test of these two predictors is stat. sig.
<class 'statsmodels.stats.contrast.ContrastResults'>
<F test: F=325.9206432972666, p=1.0499509223096256e-133, df_denom=4.96e+03, df_num=2>

As the \(p\)-value is low, we reject the null hypothesis, i.e., at least one of the predictors among mpg and year has a statistically significant relationship with car price.

Predict the car price for the cars in the test dataset. Datasets to be used: Car_features_test.csv, Car_prices_test.csv

testf = pd.read_csv('./Datasets/Car_features_test.csv')
testp = pd.read_csv('./Datasets/Car_prices_test.csv')

2.1.3 Prediction

pred_price = model.predict(testf)

Make a visualization that compares the predicted car prices with the actual car prices

sns.set(font_scale=1.25)
sns.scatterplot(x = testp.price, y = pred_price, color = 'orange')
#In case of a perfect prediction, all the points must lie on the line x = y.
ax = sns.lineplot(x = [0,testp.price.max()], y = [0,testp.price.max()],color='blue') #Plotting the line x = y.
plt.xlabel('Actual price')
plt.ylabel('Predicted price')
plt.ylim([-10000, 160000])
ax.yaxis.set_major_formatter('${x:,.0f}')
ax.xaxis.set_major_formatter('${x:,.0f}')
plt.xticks(rotation=20);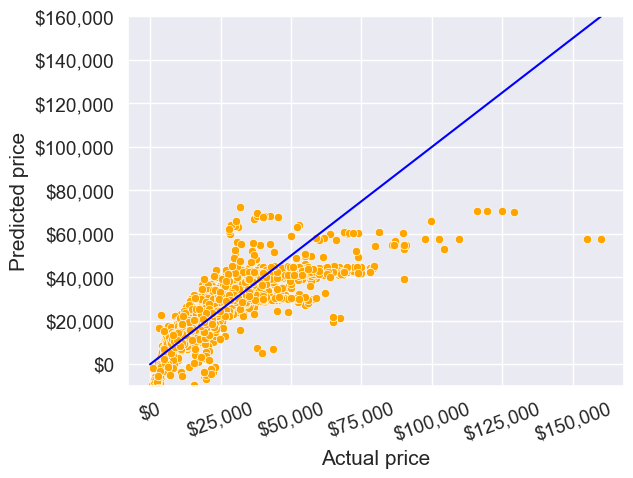

The prediction looks better as compared to the one with simple linear regression. This is because we have four predictors to help explain the variation in car price, instead of just one in the case of simple linear regression. Also, all the predictors have a significant relationship with price as evident from their p-values. Thus, all four of them are contributing in explaining the variation. Note the higher values of \(R^2\) as compared to the one in the case of simple linear regression.

What is the RMSE of the predicted car price?

np.sqrt(((testp.price - pred_price)**2).mean())
9956.82497993548

What is the residual standard error based on the training data?

np.sqrt(model.mse_resid)
9563.74782917604
trainp.describe()
carID price
count 4960.000000 4960.000000
mean 15832.446169 23469.943750
std 2206.717006 16406.714563
min 12002.000000 450.000000
25% 13929.250000 12000.000000
50% 15840.000000 18999.000000
75% 17765.750000 30335.750000
max 19629.000000 145000.000000 
sns.scatterplot(x = model.fittedvalues, y=model.resid,color = 'orange')
ax = sns.lineplot(x = [pred_price.min(),pred_price.max()],y = [0,0],color = 'blue')
plt.xlabel('Predicted price')
plt.ylabel('Residual')
ax.yaxis.set_major_formatter('${x:,.0f}')
ax.xaxis.set_major_formatter('${x:,.0f}')
plt.xticks(rotation=20);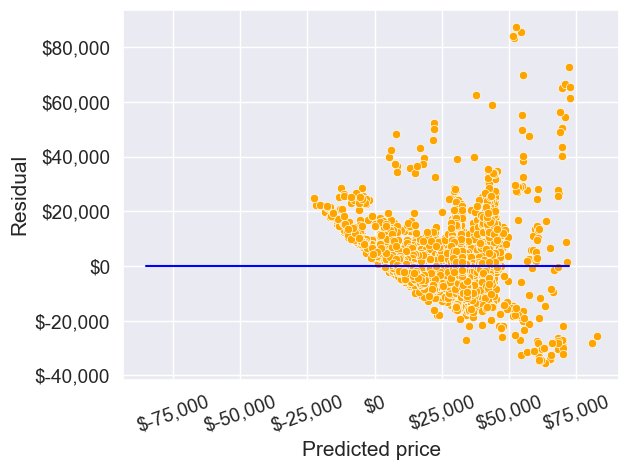

2.1.4 Effect of adding noisy predictors on \(R^2\)

Will the explained variation (R-squared) in car price always increase if we add a variable?

Should we keep on adding variables as long as the explained variation (R-squared) is increasing?

#Using the ols function to create an ols object. 'ols' stands for 'Ordinary least squares'
np.random.seed(1)
train['rand_col'] = np.random.rand(train.shape[0])
ols_object = smf.ols(formula = 'price~year+mileage+mpg+engineSize+rand_col', data = train)
model = ols_object.fit()
model.summary()
OLS Regression Results
Dep. Variable: price R-squared: 0.661
Model: OLS Adj. R-squared: 0.660
Method: Least Squares F-statistic: 1928.
Date: Tue, 27 Dec 2022 Prob (F-statistic): 0.00
Time: 01:07:38 Log-Likelihood: -52497.
No. Observations: 4960 AIC: 1.050e+05
Df Residuals: 4954 BIC: 1.050e+05
Df Model: 5
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept -3.662e+06 1.49e+05 -24.600 0.000 -3.95e+06 -3.37e+06
year 1818.1672 73.753 24.652 0.000 1673.578 1962.756
mileage -0.1474 0.009 -16.809 0.000 -0.165 -0.130
mpg -79.2837 9.338 -8.490 0.000 -97.591 -60.976
engineSize 1.218e+04 189.972 64.109 0.000 1.18e+04 1.26e+04
rand_col 451.1226 471.897 0.956 0.339 -474.004 1376.249
Omnibus: 2451.728 Durbin-Watson: 0.541
Prob(Omnibus): 0.000 Jarque-Bera (JB): 31040.331
Skew: 2.046 Prob(JB): 0.00
Kurtosis: 14.552 Cond. No. 3.83e+07


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 3.83e+07. This might indicate that there are
strong multicollinearity or other numerical problems.

Adding a variable with random values to the model (rand_col) increased the explained variation (\(R^2\)). This is because the model has one more parameter to tune to reduce the residual squared error \((RSS)\). However, the \(p\)-value of rand_col suggests that its coefficient is zero. Thus, using the model with rand_col may give poorer performance on unknown data, as compared to the model without rand_col. This implies that it is not a good idea to blindly add variables in the model to increase \(R^2\).